FPGA-Accelerated Signed Distance Field (SDF)

Signed Distance Fields (SDF) represent the distance from a given point in space to the nearest surface of a shape or object. The “signed” aspect indicates that this distance is positive when the point is outside the object and negative when it is inside. This allows the SDF to convey not just the proximity to an object’s surface, but also the positional relationship of the point relative to the object’s boundary.

In this project, we focused on generating Signed Distance Fields using Xilinx FPGA in real-time. These calculations are common in robot motion planning, obstacle avoidance, and computer graphics.

The CPU Approach

We explored two approaches for calculating Signed Distance Fields:

1. Naive Solution: Calculates the distance from a point to every surface point of an object and then selects the minimum distance. This method is simple to implement but can be computationally expensive, especially for complex objects or high-resolution fields.

2. Hill Climb Solution: The hill climb algorithm starts with an initial solution and iteratively makes small changes, each time moving towards a solution that is closer to the object’s surface. The process continues until no further improvements can be made or a certain condition is met. Since the objects in the scene are convex, the iteration eventually converges to the closest point.

The Case for Using FPGA

The Hill Climb solution offers a significant performance advantage over the naive approach by only accessing and computing vertices on the search path. This approach, however, is inherently sequential and varies in the number of iterations needed to converge across the grid. This variability makes it a suitable case for FPGA implementation, where GPUs fall short.

Design Space Exploration

Implementing the SDF calculation on an FPGA required careful consideration of several design parameters:

1. Algorithm
   • Choice between Naive or Hill Climb approaches, with Hill Climb offering better convergence patterns for convex objects
2. Local Memory
   • Whether to load grid positions and mesh data (CSR representation) to FPGA local memory for faster access
3. Tiling
   • Optimizing tile size for grid position inputs and SDF outputs to maximize memory bandwidth utilization
4. Reordering Loops
   • Decision between traversing the mesh graph or iterating the tile in inner/outer loop positions to improve locality
5. Pipelining
   • Whether to pipeline the loops when iterating over vertex neighbors to increase throughput
6. Unrolling
   • Determining the optimal number of threads for processing a tile to balance resource usage and performance
7. Load Balancing
   • Implementing load balancing strategies for threads processing different grid positions with varying convergence times
8. Temporal Locality
   • Leveraging warm-starting traversals using previous vertex information to exploit temporal coherence

These design choices significantly influenced the performance characteristics of our implementation and allowed us to optimize for both latency and energy efficiency.

FPGAs, with their reconfigurable logic, enable fine-grained load balancing across parallel cores. This adaptability allows FPGAs to maintain high efficiency and utilization, as they can dynamically redistribute tasks (job stealing) to manage points in space requiring different numbers of iterations. This feature is particularly advantageous for algorithms like Hill Climb, where workload variability is a key challenge.

FPGA Implementation

Please refer to the following slides for the FPGA implementation details:

Performance & Efficiency Advantages

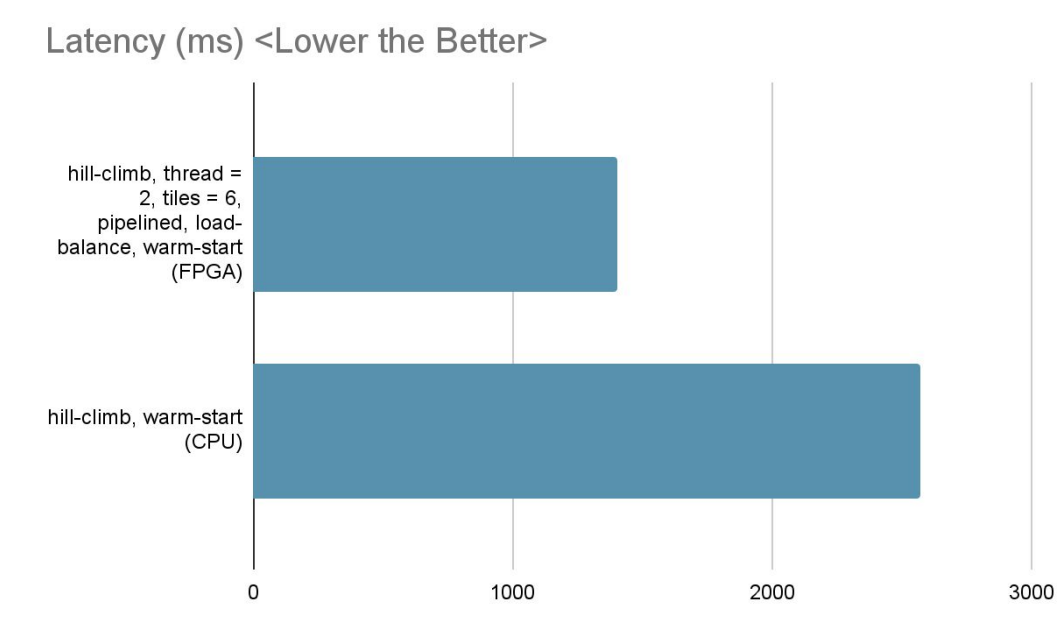
We achieved a significant reduction in latency (45.4% lower) on the Ultra96v2 board at 150 MHz compared to a sequential CPU at 1.5 GHz on the test scene.

Applications and Limitations

Why this work may be useful

In robotics, where SDF calculation latency is critical, this FPGA-based solution offers a hardware-accelerated, energy-efficient alternative. Unlike GPUs, which might perform better by processing more grid points simultaneously but consume more energy, the FPGA can leverage the algorithmic efficiency of hill climbing methods. This makes FPGAs particularly suitable for scenarios demanding both high performance and energy efficiency, as they can optimize SDF calculations effectively without the energy intensity of brute-force GPU approaches.

Why this work may not be useful

In preliminary benchmarks, a brute-force GPU implementation on an RTX 3060 has proven faster than the FPGA solution. This comparison must also consider the extra human effort required for design space exploration when adapting the algorithm to new FPGA hardware. This process, necessary for optimizing performance on different FPGA platforms, can be time-consuming.